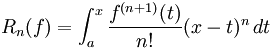4.7 - Calculo de Integrales de funciones expresadas como serie de Taylor.

En cálculo, el teorema de Taylor, recibe su nombre del matemático británico Brook Taylor, quien lo enunció con mayor generalidad en1712, aunque previamente James Gregory lo había descubierto en 1671. Este teorema permite obtener aproximaciones polinómicas de una función en un entorno de cierto punto en que la función sea diferenciable. Además el teorema permite acotar el error obtenido mediante dicha estimación

Este teorema permite aproximar una función derivable en el entorno reducido alrededor de un punto a: Є (a, d) mediante un polinomio cuyos coeficientes dependen de las derivadas de la función en ese punto. Más formalmente, si n ≥ 0 es un entero y f una función que es derivable n veces en el intervalo cerrado [a, x] y n+1 veces en el intervalo abierto (a, x), entonces se cumple que:

Donde k denota el factorial de k, y Rn es el resto, término que depende de a y es pequeño si a está próximo al punto a. Existen dos expresiones para a que se mencionan a continuación:

fdonde a y x, pertenecen a los números reales, n a los enteros y epsilon es un número real entre a y x:^[2]

Si Rn (f) es expresado de la primera forma, se lo denomina Término complementario de Lagrange, dado que el Teorema de Taylor se expone como una generalización del Teorema del valor medio o Teorema de Lagrange, mientras que la segunda expresión de R muestra al teorema como una generalización del Teorema fundamental del cálculo integral.

Para algunas funciones f(x), se puede probar que el resto, Rn (f), se aproxima a cero cuando n se acerca al ∞; dichas funciones pueden ser expresadas como series de Taylor en un entorno reducido alrededor de un punto a y son denominadas funciones analíticas.

El teorema de Taylor con Rn(f) expresado de la segunda forma es también válido si la función F tiene números complejos o valores vectoriales. Además existe una variación del teorema de Taylor para funciones con múltiples variables.

Caso de varias variables

El teorema de Taylor anterior (1) puede generalizarse al caso de varias variables como se explica a continuación. Sea B una bola en R^N centrada en el punto a, y f una función real definida sobre la clausura, cuyas derivadas parciales de orden n+1 son todas continuas en cada punto de la bola. El teorema de Taylor establece que para cualquier x Ƹ B

Donde la suma se extiende sobre los multi-índices α (esta fórmula usa la notación multi-índice). El resto satisface la desigualdad:

para todo α con |α|=n+1. Tal como sucede en el caso de una variable, el resto puede expresarse explícitamente en términos de derivadas superiores (véase la demostración para los detalles).

4.4 – Radio de Convergencia.

En matemáticas, según el teorema de Cauchy-Hadamard, el radio de convergencia de una serie de la forma viene dado por la expresión:

]

Si nos limitamos al conjunto de los números reales, una serie de la forma:recibe el nombre de serie de potencias centrada en x0. La serie converge absolutamente para un conjunto de valores de x que verifica que:

donde r es un número real llamado radio de convergencia de la serie. Esta converge, pues, al menos, para los valores de  pertenecientes al intervalo (x0-r,x0+r) , ya que la convergencia para los extremos de este ha de estudiarse aparte, por lo que el intervalo real de convergencia puede ser también semi abierto o cerrado. Si la serie converge solo para x0, r=0, Si lo hace para cualquier valor de x, r=infinito.

Radio de convergencia finito

La función  en su desarrollo con centro 0, o sea, en series de potencia: tiene el siguiente aspecto:    (para el cálculo de la serie vea serie de Taylor). Su radio de convergencia es R=1. Eso significa que para calcular si tomo cualquier valor cuya distancia al xo=0 es menor que r=1, por ejemplo el x=.25, entonces al remplazarlo en la serie el resultado de calcular la serie será el mismo que remplazarlo en la función, de hecho  (la cuenta se puede hacer por serie de potencia). Y por otro lado   Pero si tomamos un elemento fuera del radio de convergencia, por ejemplo el x=2, los más probable es que al remplazarlo en la serie, ésta diverja (por eso el nombre de radio de convergencia).

 Efectivamente:  

Radio de convergencia infinito

Por ejemplo, la función e^x puede desarrollarse en series de potencia de x-0=x, de hecho  y esto vale para todo real x por eso el radio de convergencia será infinito.

4.5 – Serie de Taylor.

En matemáticas, una serie de Taylor es una representación de una función como una infinita suma de términos.
Términos que se calculan a partir de las derivadas de la función para un determinado valor de la variable (respecto de la cual se deriva), lo que involucra un punto específico sobre la función.

La serie de una función real o compleja ƒ(x) infinitamente diferenciable en el entorno de un número real o complejo a es la siguiente serie de potencias

que puede compactarse de la siguiente manera: 

donde n! denota el factorial de n y ƒ ⁽ⁿ⁾(a) la derivada enésima de ƒ evaluada para el valor a.

Si esta serie converge para todo x perteneciente al intervalo (a-r, a+r) y la suma es igual a f(x), entonces la función f(x) se llama analítica. Para comprobar si la serie converge a f(x), se suele utilizar una estimación del resto del teorema de Taylor.
Se suele aproximar una función mediante un número finito de términos de su serie de Taylor. El Teorema de Taylor facilita la estimación cuantitativa del error de dicha aproximación. Se denomina polinomio de Taylor al número finito de los términos iniciales de la serie de Taylor de una función. La serie de Taylor de una función es, en caso de existir, el límite del polinomio de Taylor de esa función. Una función puede no ser igual a la serie de Taylor ni siquiera convirgiendo tal serie para cada punto. Una función igual a su serie de Taylor en un intervalo abierto (o un disco en el plano complejo) se denomina función analítica.

A medida que aumenta el grado del polinomio de Taylor, se aproxima a la función. Se ilustran las aproximaciones de Taylor a sen(x), centradas en 0, de grados 1, 3, 5, 7, 9, 11 y 13.

La serie de Taylor de una función f real o compleja ƒ(x) infinitamente diferenciable en el entorno de un número real o complejo a es la siguiente serie de potencias:

que puede ser escrito de una manera más compacta como la siguiente sumatoria:

4.3 Serie de potencias.

Una serie de potencias alrededor de x=0 es una serie de la forma:

Una serie de potencias alrededor de x=c es una serie de la forma:

En el cual el centro es c, y los coeficientes  son los términos de una sucesion.

4.2- Serie numérica y convergencia Prueba de la razón (criterio de D’alembert) y Prueba de la raíz (criterio de Cauchy).

El Criterio de d'Alembert se utiliza para determinar la convergencia o divergencia de una serie de términos positivos cualquiera.

Definiendo con n a la variable independiente de la sucesión, dicho criterio establece que si llamamos L al límite para n tendiendo a infinito de  An+1/An se obtiene un numero L:

El criterio de D'Alembert se utiliza para clasificar las series numéricas. Podemos enunciarlo de la siguiente manera: Sea: 

Tal que:

§  f(n) > 0 (o sea una sucesión de terminos positivos) y

§  f(n) tienda a cero cuando n tiende a infinito (condición necesaria de convergencia)

Se procede de la siguiente manera:  

Así obtenemos L y se clasifica de la siguiente manera: 

§  L < 1 la serie converge

§  L > 1 la serie diverge

§  L = 1 el criterio no sirve hay que aplicar otro criterio.

   Criterio de Cauchy (raíz enésima)

   Sea una serie  

  tal que a_k > 0 (serie de términos positivos). Y supongamos que existe.

Entonces, si:

§  L < 1, la serie es convergente.

§  L > 1 entonces la serie es divergente.

§  L=1, no podemos concluir nada a priori y tenemos que recurrir al criterio de Raabe, o de comparación, para ver si podemos llegar a alguna conclusión.

Carlos, Emmanuel y Rodrigo te ayudan.

Hola! te damos la bienvenida a este tu espacio donde podrás aprender muchisimas calculo! :D nosotros alumnos de tercer semestre del Instituto Tecnológico de Piedras Negras preocupados por ayudar, crean este blog con el único fin de compartir un poco del conocimiento adquirido a lo largo del curso de calculo integral.

"El único obstáculo para lograr nuestras metas, somo nosotros mismos."

bueno comenzaremos con el primer tema como marca el programa de nuestra materia en esta cuarta unidad que es:

4.1- Definición de Serie (Serie finita e infinita).

4.1 Definicion de serie: 4.1.1 Finita, 4.1.2 Infinita (Criterio de D' Alembert) (Criterio de Cauchy)

4.1 Definicion de serie
Definiciones y notación.

A la suma de una sucesión de términos se denomina SERIE y el valor de dicha suma, si es que tiene
alguno, se define como

S = lim S n .
n→∞
Un ejemplo de serie infinita, denominada así debido a que dicha sucesión es infinita, es la
denominada serie geométrica, la cual se obtiene a partir de un térmno inicial
multiplicado por una cantidad constante, p. ej.
a + ar + ar 2 + ar 3 + ⋅ ⋅ ⋅ + ar n −1 + ⋅ ⋅ ⋅ . En
este caso la cantidad inicial a es multiplicada por la cantidad constante r para obtener dicha
serie infinita.
En general una serie infinita significa una expresión de la forma
a1 + a2 + a3 + ⋅ ⋅ ⋅ + an + ⋅ ⋅ ⋅ ,
donde las an son números o funciones dadas por alguna regla o fórmula. Los tres puntos
significan que la serie nunca termina. Si se tiene duda de cómo es la regla usada en la
formación e la serie, el término general o término n-ésimo deberá expresarse, p. ej.
12 + 2 2 + ⋅ ⋅ ⋅ + n 2 + ⋅ ⋅ ⋅
x − x 2 + x
2
+ ⋅ ⋅ ⋅ +
(− 1)n−1 x n
(n − 1)!
+ ⋅ ⋅ ⋅
También usaremos formas abreviadas para denotar las series, p. ej. para las series anteriores, la
forma abreviada será




∞
∑
n=1
∞
∑ n 2
n =1
(− 1)n−1 x n
(n − 1)! .

Las aplicaciones de las series infinitas son muchas, pero mencionamos como lo más importante para
nosotros en este momentos, su uso en la solución de problemas matemáticos que no pueden resolverse
en términos de funciones elementales ( potencias, raíces, funciones trigonométricas y sus inversas,
logaritmos y exponenciales y combinaciones de estos), o en caso de que puedan resolverse, es muy
complicado trabajar con ellos. En estos casos encontramos una respuesta en función de una serie y
usamos
los términos requeridos de acuerdo a la presición deseada. Las ecuaciones diferenciales son
resueltas en muchas ocasiones en función de series infinitas. Una integral definida,
0.1
por ejemplo,
∫ e − x
0
dx , para la cual no hay solución en términos de funciones
elementales, se puede resolver su expandiendo su integrando en una serie e integrando término a
término dicha serie.